Index

• Part 1 - Recursive anonymous functions
• Part 2 - The code problem
• Part 3 - A recursive Y Combinator
• Part 4 - Non-recursive Y Combinator

TL;DR: just show me the code.

Non-recursive Y Combinator

Enjoyed your beer? Let’s get started.

There are several ways to get to the non-recursive Y.
An approach, magnificently covered in Scheme by professor Michael Vanier in The Y Combinator (Slight Return), is to start over from the original recursive sum function, to extract mkSum and then to inject mkSum into itself. In C# it does not translate to the easiest path, but if you feel up for the challenge, go down the rabbit hole reading Recursive Y Combinator in C# - alternative approach.

A shorter and possibly more intuitive plan of attack is to directly play with the recursive Y we got in Part 3

static Func<Func<Sum, Sum>, Sum> Y =
  f =>
    n =>
      f(Y(f))(n);

refactoring the recursion away. This will require injecting a function into itself, just like in Michael Vanier’s approach, only at an earlier stage.
Let’s get started.

• Step 1 - Extract Y to a local function
  • Make n => f(Y(mkSum))(n) a variable
  • Extract a local function
  • Get rid of the temporary variable
• Step 2 - Replace Y(mkSum) with sub
• Step 3 - Inject self
  • Replace sub with self
• Step 4 - Replace variable with lambda
  • Variables are just syntactic sugar of lambda expressions
  • Replace sub(sub) with lambda
• Step 5 - Inline sub

Step 1 - Extract Y to a local function

As we anticipated, in order to eliminate the recursion, in our refactoring journey we will eventually inject a function into itself. From f() to f(f). We cannot do this directly with Y, though, because its signature must be preserved.
So, we’d better create a bottleneck, extracting Y to a local function.

It’s easy to see that R# is not able to do that: if you select n => f(Y(mkSum))(n) and you apply Extract Local Function, R# would default to Extract Method instead. It’s probably a bug.
We have to do this manually, in 3 steps, using a temporary variable:

• Introduce a temporary variable
• Extract a local function
• Get rid of the temporary variable

Make n => f(Y(mkSum))(n) a variable

Select n => f(Y(f))(n) and apply Introduce Variable:

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sum1 = n => f(Y(f))(n);
    return sum1;
}

Extract a local function

Select n => f(Y(mkSum))(n) and Extract a Local Function out of it (funny enough, now R# does not complain):

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub() =>
        n => f(Y(f))(n);

    Sum sum1 = sub();
    return sum1;
}

Get rid of the temporary variable

Target sum1 and apply Inline Variable to get rid of it:

private static readonly Sum sum =
    Y(mkSum);

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub() =>
        n => f(Y(f))(n);

    return sub();
}

Voilà! We have Y in a local function. We can now play with sub() and safely change its signature with no impacts on the Y(mkSum) calling site.

Step 2 - Replace Y(f) with sub()

Focus on f(Y(f))(n).
By definition, Y(f) returns sub(). So, we can easily replace one with the other. Wherever you see Y(f), replace it with sub():

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub() =>
        n => f(sub())(n);

    return sub();
}

Is the test still green? Yes, it is! That’s because sub() is lazy, and it does not fall into any stack overflow. This should clarify why in Step 1 we extracted the lazy n => f(Y(mkSum))(n) rather than the eager f(Y(mkSum)).

Is this a non-recursive Y? Not yet. Indeed, sub() is still recursive.
But we are almost there! Get ready, we are going to perform the most crucial step: removing the recursion.

Step 3 - Inject self

Let’s inject a continuation into sub(). What would the perfect continuation be? But of course, sub itself! Here we are: that’s the announced step where we inject a function into itself.

Injecting a function into itself is not like calling a function from itself: the latter is the classical recursion; the former is almost recursion, it’s Continuation Passing Style.
So, our next goal is to make sub a parameter of itself, which will make sub not recursive, just almost.

Again, R# will not help us. This time, as we will see, we can forgive it.

Let’s focus on sub:

    Sum sub() =>
        n => f(sub())(n);

sub is of type Func<Sum>. Ideally, selecting sub we should be able to make it a variable, getting something like:

    Sum sub()
    {
        var v = sub;
        return n => f(v())(n);
    }
        

If you try, though, you will get a depressing:

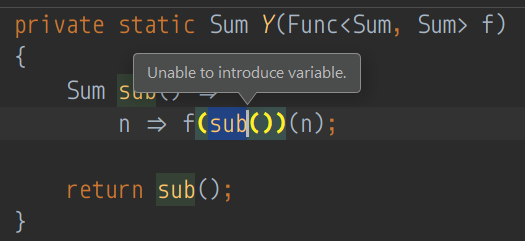
Can you guess why? It will be clear very soon.
Trying to make sub a parameter of itself with Introduce Parameter fails even more cryptically: R# would just ignore the keybinding. Definitely, we are taking R# to its limit. We have to do this manually.

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub(??? self) =>
        n => f(sub(self))(n);

    return sub(sub);
}

Ok, this one is tricky. Let’s comment what we have written:

• Sub sub() => ... gets a new parameter, which we called self. So it’s now Sum sub(??? self) => ....
  Besides the unknown type we marked with ???, this makes sense, doesn’t it?
• In n => f(sub(self)(n), we are correctly feeding sub with the continuation self;
• return sub() becomes return sub(sub) because we are providing sub with itself as a continuation.

All good.

The only big deal is: what’s the type of self? What to replace ??? with?
By definition, self = sub, and sub was of type Func<Sum>. Notice we say “it was”. Indeed, now sub takes a parameter of (still unknown) type ???, so its type changed to from Func<Sum> to Func<???, Sum>.
??? is the type of sub. So, inlining, we get to Func<Func<???, Sum>, Sum>; if we continue inlining, we get Func<Func<Func<???, Sum>, Sum>, Sum>, the Func<Func<Func<Func<???, Sum>, Sum>, Sum>, Sum> and so on, ab nauseam.
It’s Func all the way down…

Smells like recursion, doesn’t it?

In fact, sub’s type is recursive. No surprises, after all, if R# was not able to realize that.
Let’s define a recursive type manually:

private delegate Sum Rec(Rec self);

With this we can define:

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub(Rec self) =>
        n => f(sub(self))(n);

    return sub(sub);
}

Compilation’s OK.
Test’s green.
Wow, that’s a result.

Replace sub with self

self is sub. Then sub(self) = self(self):

private delegate Sum Rec(Rec self);

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub(Rec self) =>
        n => f(self(self))(n);

    return sub(sub);
}

Take your time to meditade on the last snippet:

• It is non-recursive
• It’s a combinator: that is, it’s a pure function, only depending on its own parameters.
• More thatn this, is has got the same signature of our ideal Y Combinator
• It passes our tests

You know the saying “If it walks like a duck”?
Is that, maybe, the non-recursive Y Combinator, already? Oh, yes it is!
But it’s not yet in a form worth to be tattooed on your forearm. Let’s just perform a last little effort to refactor it to its canonical shape. Then you are ready to schedule an appointment to your preferred tattoo shop.

Step 4 - Replace variable with lambda

The last snippet has got 2 little problems.

The first one is: we would like to have a single, fluent expression, with no local functions. That’s easy: we just have to inline sub.

The second problem is: sub is mentioned twice in return sub(sub). Inlining sub would produce an insulting:

private static Sum Y(Func<Sum, Sum> f) =>
    n1 => f(((Rec)(self => n => f(self(self))(n)))(self => n => f(self(self))(n)))(n1);

You would never tattoo this: you don’t have enough long forearms, do you?
Ok. We need a last little trick. We need to learn how to replace variables with lambda expressions. We have to convince ourselves that:

sub(sub)

is equivalent to

new Func<Rec, Sum>(f => f(f))(sub)

where sub is mentioned only once.
Now, this deserves a little explanation, right?

Variables are just syntactic sugar of lambda expressions

This refactoring move is easily done once we realize that variables are just syntactic sugar for lambda expressions. This will not surprise our fellow Lisp programmer. In C# we could observe that:

var foo = 42;

can be written with a lambda expression followed by its invocation:

Func<int> f = x => x;

var foo = f(42);

that inlined becomes

var foo =
    ((Func<int>)(x => x))
        (42)

This also works with more complex expressions:

int F(int i)
{
    var foo = 42;
    return (foo + i)*2;
}

becomes

int F(int i)
{
    return 
        ((Func<int>)(foo => 
            (foo + i)*2*))
        (42);
}

Finally, this also works with multiple parameters:

static int F()
{
    var name = "John";
    var surname = "Doh";
            
    return $"Hi, {name} {surname}!";
}

F().Should().Be("Hi, John Doe!");

can be converted to:

static int F()
{
    return
        ((Func<string, string, string>)(
            (name, surname) =>
                $"Hi {name} {secondName}!"))
        ("John", "Doh")
}

Pretty neat, isn’t it? If you want to learn how to perform these transformations only using refactoring moves, go read Refactoring variables to lambda expressions

Replace sub(sub) with lambda

Good, let’s apply this to return sub(sub).

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub(Rec self) =>
        n => f(self(self))(n);

    return sub(sub);
}

becomes:

private static Sum Y(Func<Sum, Sum> f)
{
    Sum sub(Rec self) =>
        n => f(self(self))(n);

    return Func<Rec, Sum>(f => f(f))(sub);
}

where sub is mentioned only once.

Step 5 - Inline sub

Now inlining sub we get a nice looking:

private static Sum Y(Func<Sum, Sum> f) =>
    new Func<Rec, Sum>(f =>
        f(f))
    (self =>
        n =>
            f(self(self))(n));

This is the Y Combinator. Feel proud of yourself, we made it.

Conclusion

If we only could get rid of the boiler plate code C# requires, this would be:

var Y = f =>
    (f => f(f))(self => f(self(self));

var sum = Y(mySum);

which is equivalent to the original Lisp’s Y Combinator:

(define Y
  (lambda (f)
    ((lambda (x) (x x))
     (lambda (x) (f (lambda (y) ((x x) y)))))))

Cool. Mission accomplished. You deserve a second beer.

Prosit!

References

• JetBrains Refactorings
  • Extract Method
  • Introduce Parameter
  • Inline Variable
  • Inline Method
  • Context Actions
  • Move Variable To Outer Scope
  • Move Local Function To Outer Scope
• Continuation Passing Style
• Refactoring variables to lambda expressions
• Variables Just Are Syntactic Sugar For Lambda Expressions
• Continuation Passing Style
• Combinator - Haskell Wiki