Deriving the Y Combinator in C# - Part 3 - A recursive Y Combinator
Index
- Part 1 - Recursive anonymous functions
- Part 2 - The code problem
- Part 3 - A recursive Y Combinator
- Part 4 - Non-recursive Y Combinator
TL;DR: just show me the code.
Recursive Y Combinator
- Step 1 - An ordinary recursive function
- Step 2 - Inject a continuation
- Step 3 - Define Y with Extract Method
Step 1 - An ordinary recursive function
We will get to Y progressively, transforming the original sum function with a series of refactoring moves. This means that, along the way, we will neither break the compilation nor the observable behavior of sum.
As a safety net, we can use a FsCheck property test: it will make sure that, while refactoring, sum will always keep satisfying the well known Gauss Formula:
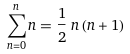
public class YCombinator
{
private const int Max = 12_000;
private readonly Arbitrary<int> PositiveNumbers = Arb.From(Gen.Choose(0, Max));
private static readonly Func<int, int> sum =
n =>
n == 0 ? 0 : n + sum(n - 1);
[Property]
Property it_meets_the_gauss_formula() =>
ForAll(PositiveNumbers, n =>
sum(n) == n * (n + 1) / 2);
}
(For a fun introduction to Property Testing, I can only recommend the brilliant The lazy programmer’s guide to writing thousands of tests by Scott Wlaschin)
Notice that we have to limit the test input space to the first 12.000 positive numbers: differently from F#, C# does not have any tail-recursion optimization; exceeding that value would overflow the stack, crashing the test with an exception.
Type alias
Let’s replace Func<int, int> with the type alias Sum, using a delegate:
private delegate int Sum(int n);
private static readonly Sum sum =
n =>
n == 0 ? 0 : n + sum(n - 1);
Be aware though that, while delegates can make the code a bit less verbose, they get in the way of the compiler type inference.
Step 2 - Inject a continuation
As we saw before, we can remove the recursion from sum by letting it invoke a continuation instead of itself.
The goal is to define a sum-generating function, MkSum, of type Func<Sum, Sum> that, given a continuation of type Sum, generates a sum function of type Sum.
Why are we doing this? Remember what we commented in part 2 - Feeding itself with itself: MkSum is able to create sum, if only it is given a sound continuation, and sum is by definition a sound continuation. The idea is then to feed MkSum with its own result.
Of course, in order to do that, we have to make MkSum a thing, we need to extract it.
Define MkSum with Extract Method
Let’s apply Extract Method to n => n == 0 ? 0 : n + sum(n - 1) to define MkSum:
delegate int Sum(int n);
static readonly Sum sum =
MkSum();
static Sum MkSum() =>
n =>
n == 0 ? 0 : n + sum(n-1);
This creates what Matteo Baglini calls a bottleneck: a single place in the source code from which to operate a refactoring change.
Let sum float up
We have to replace sum in MkSum with a continuation. Let’s pull it up applying Introduce Parameter:
delegate int Sum(int n);
static readonly Sum sum =
MkSum(sum);
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
We still have recursion, but somehow we highlighted that we are using sum as a continuation.
Make sum lazy
Surprisingly, running the test we get a NullReferenceException. Ideally, an automated refactoring move performed by the IDE should be guaranteed to preserve the behavior. As we see, this is not always the case.
The problem here is the way sum is defined: it’s a field, not a method.
static readonly Sum sum =
MkSum(sum);
When the value of sum is being evaluated, MkSum is invoked with its parameter sum, which is fatally still null. That’s a consequence of C#’s eager evaluation of statements. We can make sum lazy defining it as a method or, alternatively, as a lambda, abandoning the point-free style:
delegate int Sum(int n);
static readonly Sum sum =
n =>
MkSum(sum)(n);
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
Unfortunately, the test will still fail, this time for a stack overflow. In fact, we added one extra layer of indirection, which increased the stack usage. We need to compensate the problem shrinking the range of numbers used by the property test:
public class YCombinator
{
private const int Max = 8_000;
private readonly Arbitrary<int> PositiveNumbers = Arb.From(Gen.Choose(0, Max));
[...]
This passes the test.
OK. It’s time to finally define Y.
Step 3 - Define Y with Extract Method
Let’s create again a bottleneck, applying Extract Method to MkSum(sum):
delegate int Sum(int n);
delegate Sum MkSum(Sum continuation);
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
static Sum Y() =>
MkSum(sum);
static readonly Sum sum =
n =>
Y()(n);
Inject MkSum as a parameter
In the second installment we described Y as a function to be used as:
Sum sum = Y(quasi_sum);
We can get to this applying Introduce Parameter to MkSum:
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
static Sum Y(Func<Sum, Sum> f) =>
f(sum);
static readonly Sum sum =
n =>
Y(MkSum)(n);
Move laziness from sum to Y
We can make Y lazy and revert sum to eager and point-free:
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
static Sum Y(Fun<Sum, Sum> f) =>
n =>
f(sum)(n);
static readonly Sum sum =
Y(MkSum);
Replace sum with Y(MkSum)
We are almost there. Look closely to Y. It’s defined as:
static Sum Y(Func<Sum, Sum> f) =>
n =>
f(sum)(n);
We have to eliminate that sum. This is trivial, once we notice that sum is:
static readonly Sum sum =
Y(MkSum);
If sum = Y(MkSum) and Y = f(sum), then Y = f(Y(MkSum)), and since f = MkSum, this can be finally simplified as Y = f(Y(f)).
Ideally, we could do this applying Inline Method. Unfortunately, we have to do this manually: R# has got a bug and does not allow inlining only one specific usage.
delegate int Sum(int n);
static Sum MkSum(Sum continuation) =>
n =>
n == 0 ? 0 : n + continuation(n-1);
static Sum Y(MkSum f) =>
n =>
f(Y(f))(n);
static readonly Sum sum =
Y(MkSum);
As a field, Y becomes:
static Func<Func<Sum, Sum>, Sum> Y = f => n => f(Y(f))(n);
We made it. This is our coveted (recursive) Y Combinator.
Conclusion
Does it work? The tests are still green.
Let’s see if it allows us to use a recursive sum function as an anonymous lambda.
Remember when we got stuck with the following?
var result = new [] { 0, 1, 2, 3, 4 }.Select(n => n == 0 ? 0 : n + ???(n - 1));
result.Should().BeEquivalentTo(new [] { 0, 1, 3, 6, 10 });
Let’s verify how our brand new recursive Y Combinator helps here. Our sum is:
Sum sum = Y(MkSum);
or, expanded:
Sum sum = Y( f => n => n == 0 ? 0 : n + f(n-1) );
Used as an anonymous function:
var result =
new [] { 0, 1, 2, 3, 4 }
.Select(i =>
Y(f => n => n == 0 ? 0 : n + f(n-1))(i));
result.Should().BeEquivalentTo(new [] { 0, 1, 3, 6, 10 });
Cool. We are actually using a recursive-like function (defined with Continuation Passing Style) as an anonymous lambda.
If you want to simplify to:
new [] { 0, 1, 2, 3, 4 }.Select(
Y(f => n => n == 0 ? 0 : n + f(n-1));
you have to give up the Sum type alias, which makes it clear that C# delegates are a poor way to aliasing types.
Non-recursive Y Combinator
Is that all?
Meh. I don’t know you, but I feel like I cheated. Afterall, we extracted the recursion away from the original function, only to push it inside Y. It is a result. But it stinks, it’s sweeping the dust under the carpet. We can surely do better: we can remove the recursion altogether, distilling a stricly non-recursive Y Combinator.
This will be a bit more challenging. Take a deep breath, have a beer and when you are ready, jump to the forth and last installment.
References
- JetBrains Refactorings
- FsCheck
- Matteo Baglini - Twitter
- Continuation Passing Style - Wikipedia
- JetBrains Bug RSRP-439279: Inlining fields in usage causes all usages to be inlined
- Scott Wlaschin - The Lazy Programmer’s Guide To Writing Thousands Of Tests
- Carl Friedrich Gauss - Anecdotes - Wikipedia
- Tacit Programming - Wikipedia