Deriving the Y Combinator in C#
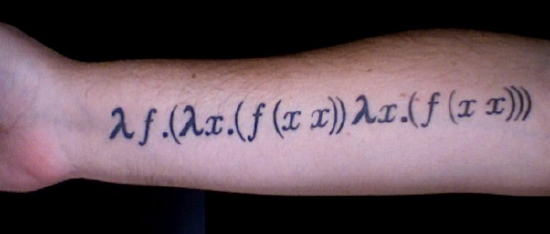
What the heck is that? That’s the Y Combinator!
Uh? A higher-order function with which anonymous lambdas can be made recursive.
Sounds useful, I guess? No, it’s not. It’s a purely intellectual challenge.
Any practical application for my C# developer daily life? Not at all.
So, what’s the point? Why? Because it’s fun.
Index
This a 4 parts article. You are reading the first installment.
- Part 1 - Recursive anonymous functions
- Part 2 - The code problem
- Part 3 - A recursive Y Combinator
- Part 4 - Non-recursive Y Combinator
TL;DR: just show me the code.
Recursive named functions
Consider a generic 1-parameter, recursive function. Let’s use for example sum(n), that returns the sum of all numbers between 0 and n. Its implementation is trivial.
static int Sum(int n) =>
n == 0 ? 0 : n + Sum(n - 1);
C# decently supports Functional Programming, so Sum can be passed as an argumento to high-order functions, even in point-free style, like in:
var result = new [] { 0, 1, 2, 3, 4 }.Select(Sum);
result.Should().BeEquivalentTo(new [] { 0, 1, 3, 6, 10 });
So far so good.
Recursive anonymous functions
Here comes a puzzling quiz: can we inline Sum? That is, can we replace Sum in Select with its own definition, as an anonymous lambda?
Spoiler: No, we can’t. If we try, we will miserably fail ending up with a disappointing:
var result = new []{0, 1, 2, 3, 4}.Select(n => n == 0 ? 0 : n + ???(n - 1));
What should the value of ??? be?
The fact is, a function can invoke itself only by name. No name, no party. It seems that there are no chances for anonymous lambdas to be recursive.
Or are there?
The Y Combinator
It might not seem immediately obvious, but this problem has to do with Fixed Points and λ-calculus. Its solution was invented (or discovered?) back in the 1940s, way before C# was a thing, by Haskell Curry.
Haskell Currry is the man the Haskell and the Curry functional programming languages and the currying coding techniques are named after. And indeed, although a mathematical concept, the Y Combinator is also a topic that can be purely tackled with code, no maths involved.
And that’s exactly what we are going to do in the second installment
References: