Index
Source code: github.com/arialdomartini/state-monad-for-the-rest-of-us.

Generic mapping

In the last chapter we challenged ourselves to generalize the 2 almost identical functions. I have already spoiled it: doing so, you will invent Functors. Let’s go started.

Let’s consider again the original function:

// Tree String -> Tree Int
let rec lengths tree =
    match tree with
    | Leaf v -> Leaf(String.length v)
    | Node(l, r) -> Node(lengths l, lengths r)

This function contains both:

• The logic for traversing a tree.
• The String.length function for perfoming the domain logic.

Instead of String.length, imagine a function that parses strings to integers:

// String -> Int
let parseWordToInt (word: string) : int =
    match word with
    | "one" -> 1
    | "two" -> 2
    | "three" -> 3
    | "four" -> 4
    ...

and one that counts the vowels in a string:

// String -> Int
let countVowels (input: string) : int =
    // we don't even care about its implementation

Since both share with String.length the same signature String -> Int, you could easily use either in your algorithm:

// String -> Int
let String.length (input: string)  int = ...

// Tree String -> Tree Int
let rec lengths tree =
    match tree with
    | Leaf v -> Leaf(parseWordToInt v)
    | Node(l, r) -> Node(String.length l, String.length r)

and

// String -> Int
let countVowels (input: string) : int = ...

// Tree String -> Tree Int
let rec lengths tree =
    match tree with
    | Leaf v -> Leaf(countVowels v)
    | Node(l, r) -> Node(algo l, algo r)

In fact, you can use any a -> b function, no matter the a and b types. It makes sense to generalize the function and abstract the action away, passing it as a parameter f. This would be akin to implementing the Strategy Pattern.

You can introduce f as a parameter either before or after tree.

Putting f after tree would get to:

// Tree String -> (String -> Int) -> Tree Int
let rec lengths tree f =
    match tree with
    | Leaf v -> Leaf(f v)
    | Node(l, r) -> Node(lengths l, lengths r)

Placing f before tree would get to:

// (String -> Int) -> Tree String -> Tree Int
let rec lengths f tree =
    match tree with
    | Leaf v -> Leaf(f v)
    | Node(l, r) -> Node(lengths l, lengths r)

Notice that the implementation is perfectly the same.

You may not have realized it, but with the simple act of introducing the f parameter you made lengths a high-order function, and you just invented Functors.
While the placement of a parameter might seem a superficial detail, it actually reflects two fundamentally different mental models. Depending if you have f as the first or as the second parameter, the signature reflects a completely different metaphor: either Functors as boxes or Functors are morphisms between categories.
This deserves some considerations, doesn’t it?

A tale of 2 metaphors

Opening Boxes

Let’s start from the version where the tree comes first:

// Tree String -> (String -> Int) -> Tree Int
let rec lengths tree f =
    match tree with
    | Leaf v -> Leaf(f v)
    | Node(l, r) -> Node(lengths l, lengths r)

Is the lengths signature still correct? Is the name lengths still reflecting the operation being performed?
Indeed, there is nothing in the implementation about calculating lengths. And, to tell the whole truth, the function is not even about strings anymore. It’s not hard to realize that the function is now generic. If you ask the F# compiler which type it infers, it will answer Tree a -> (a -> b) -> Tree b:

lengths deserves a new name. To choose one, consider the mental model you can use to interpret this signature:

• Tree a is a box containing a value of type a.
• You provide lengths with such a box, plus a function f from a to b, with the goal of applying f to the box content.
• You don’t need to open the box: lengths will do this for you, giving you back a new box, containing a tranformed content of type b.

Here’s a classic picture from Aditya Bhargava’s “Functors, Applicatives, And Monads In Pictures”:

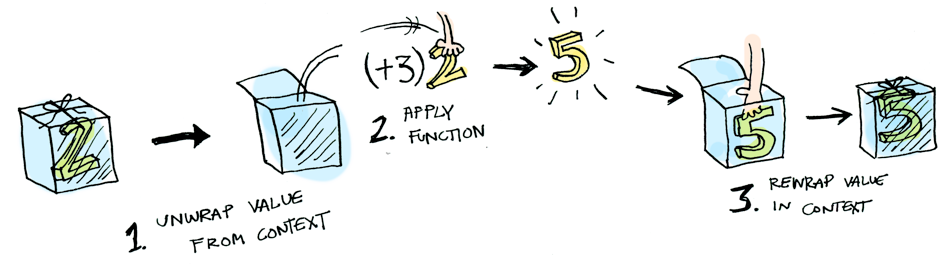
It make sense to rename this transform. LINQ calls it Select. Indeed, here’s the official signature of Select in the .NET framework:

public static IEnumerable<TResult> Select<TSource, TResult>(
            this IEnumerable<TSource> source, Func<TSource, TResult> selector)

It matches the model Box TSource -> (TSource -> TResult) -> Box TResult.
The Scala library Cats calls it map. You can verify that it has the same signature you obtained:

abstract def map[A, B](fa: F[A])(f: (A) => B): F[B]

Although this is a very popular implementation for Functors, I am not particularly fond of it, and I think it’s based on a poor metaphor.
Let me show you a more powerful metaphor, enabled flipping f and tree.

Lifting Functions

The signature (a -> b) -> Tree a -> Tree b is the one used by Haskell (see fmap on Hoogle):

// (a -> b) -> Tree a -> Tree b
let rec map f tree =
    match tree with
    | Leaf v -> Leaf(f v)
    | Node(l, r) -> Node(map f l, map f r)

The reason why this introduces a fundamentally different interpretation has to do with Currying and Partial Application. It may not be immediately apparent but, since functions associate on the right, the signature:

(a -> b) -> Tree a -> Tree b

can be written as:

(a -> b) -> (Tree a -> Tree b)

While:

// (a -> b) -> Tree a -> Tree b
let rec map f tree = ...

can be interpreted as a function taking 2 parameters and returning a Tree b, the same function with the alternative, equivalent signature

// (a -> b) -> (Tree a -> Tree b)
let rec map f = 
  fun tree -> ...

can be interpreted as a high-order function taking 1 parameter only, and returning a new function Tree a -> Tree b:

Notice how the following 2 forms are equivalent:

This is a general rule. Any F# function:

// a -> b -> c -> d -> e
let f a b c d e = ...

is completely equivalent to:

// a -> (b -> (c -> (d -> e)))
let f = 
  fun a -> 
    (fun b -> 
	  (fun c -> 
	    (fun d -> 
		  (fun e -> ...))))

This technique is called currying.
In reality, all F# (and Haskell) functions take 1 parameter only. Multi-parameter functions are an illusion, syntactic sugar based on implicitely applied currying.

These different perspectives get to two completely different interpretations:

Read again the curried form of our function:

// (a -> b) -> (Tree a -> Tree b)
let rec map f = 
  fun tree -> 
    match tree with
    | Leaf v -> Leaf(f v)
    | Node(l, r) -> Node(map f l, map f r)

You give map a humble function f: a -> b, which can only operate on a values; map transforms it into an on-steroids function superF: Tree a -> Tree b.

To see this in practice, consider again the test method:

[<Fact>]
let ``calculate the leaves' content length, using map`` () =
    let treeOfLengths = map String.length treeOfWords

    test <@ treeOfLengths = treeOfNumbers @>

and focus on

map String.length treeOfWords

It’s feeding map with 2 arguments. But we know that all functions are 1-parameter functions. What happens if you pass only 1 argument — that is, if you partially apply it? In other words, what’s the meaning of:

map String.length

Let’s see this in action:

let mapped = map String.length
let treeOfLengths = mapped treeOfWords

test <@ treeOfLengths = treeOfNumbers @>

If you ask F# to add type annotations on mapped, it would write:

let mapped: Tree<string> -> Tree<int> = map String.length
let treeOfLengths = mapped treeOfWords

test <@ treeOfLengths = treeOfNumbers @>

Read it like this: you feed map with String.length, a function String -> Int which can only operate on strings; it gives you back a super-String.length, which operates on trees of strings.
We can make this even more apparent aliasing map with a custom operator ^:

let (^) = map

Guess if the following compiles:

let treeOfLengths = String.length treeOfWords

test <@ treeOfLengths = treeOfNumbers @>

Of course it does not! String.length operates on strings, and treeOfWords is a Tree<string>, not a string. Let’s make it a function on-steroids with our brand new ^ operator:

let treeOfLengths = String.length^ treeOfWords

test <@ treeOfLengths = treeOfNumbers @>

Wow! It works!
Can you see how this is based on the metaphor of lifting functions? The idea is: you can think in terms of simple types, without worrying about trees; you just write your ordinary functions operating on ordinary types. Then, you lift your functions so they learn how to operate on trees.

Let me use again this image by Bartosz Milewski, from the chapter Functors of his book Category Theory for Programmers:

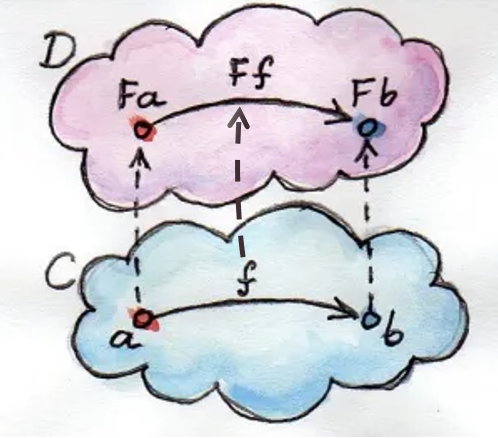
to which I added a missing arrow. Here’s the metaphor:

• There are 2 worlds: C, the lower world of ordinary functions and values; and D, the upper world of Trees.
• In the lower world of ordinary functions there is a function f from the type a to the type b. In our case, String.length.
• In the upper world of Trees, there is an on-steroids function F f that does the same of String.length, but on Trees of strings instead of just strings.
• map / ^ is that function that lifts whatever function f, operating on simple values, to the on-steroids function F f, operating on trees of simple values.

This is the notion of Functors: something able to move objects and functions from one world / category to another — possibly richer — one.
This is not a series on Category Theory, so we will stop here on this topic. It should suffice to interpret the result as follows:

• Via the implementation of map, you capture the essence of traversing a tree and applying a function to its content.
• This allows your design to completely separate the domain logic (String.length, countVowels, etc) from the tree-traversing code.
• The mental model you can use is that map lifts ordinary functions to tree-operating functions, without forcing you to re-implement the traversing logic over and over.

Cool. If you managed to read this far, take a break, reward yourself with a well deserved delicacy, and get ready to the next chapter. You are going to discover the limits of Functors.

Go to Chapter 4.

References

• State Monad For The Rest Of Us - source code
• github.com/dotnet/runtime - Signature of LINQ Select
• Signature of map in Cats
• Signature of fmap
• Aditya Bhargava - Functors, Applicatives, And Monads In Pictures
• Wikipedia - Currying
• Bartosz Milewski - Category Theory for Programmers
  • Bartosz Milewski - Functors

Comments

GitHub Discussions