In which you discover that Bind is a combinator
and you feel illuminated

If you want to understand Functors, it helps to develop a little different intuition on Monads. And in order to do so, it helps to go back to the roots. Don’t worry, it will take only few seconds.

Imagine you have 2 ordinary functions:

f :: A -> B
g :: B -> C

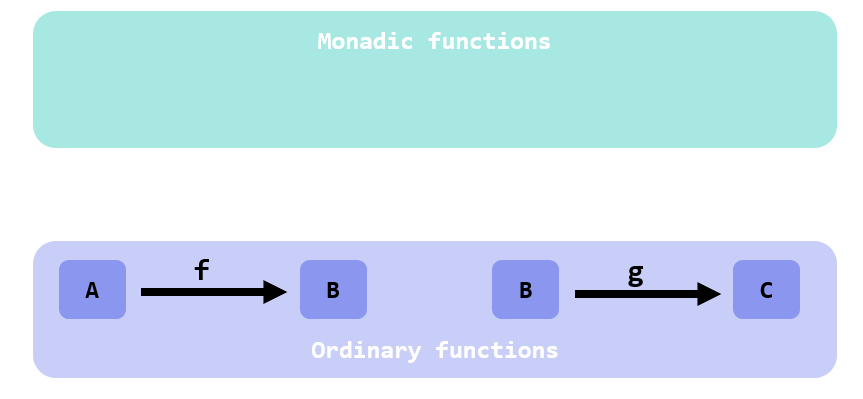
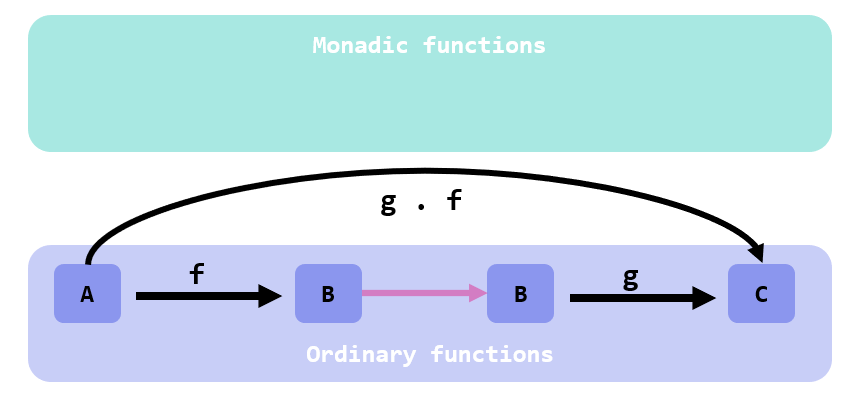
You know that they are type-compatible: the output of f has the same type of the input of g. So you can both:

• Apply f to the output of g.
• Compose f and g and build a new function g . f.

Ok, we are done with the roots. I promised it would be fast.
Let’s see now what happens with monadic functions. Suppose you have:

f :: A -> Monad<B>
g :: B -> Monad<C>

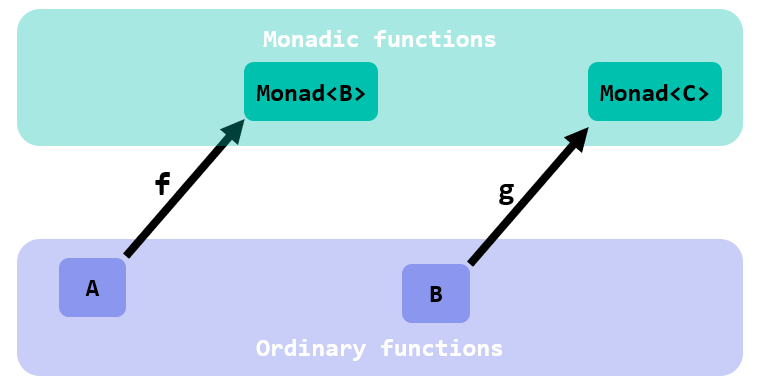
They are not type-compatible: the output of f has a different type than the type requested by g. You cannot just feed g with the output of f:

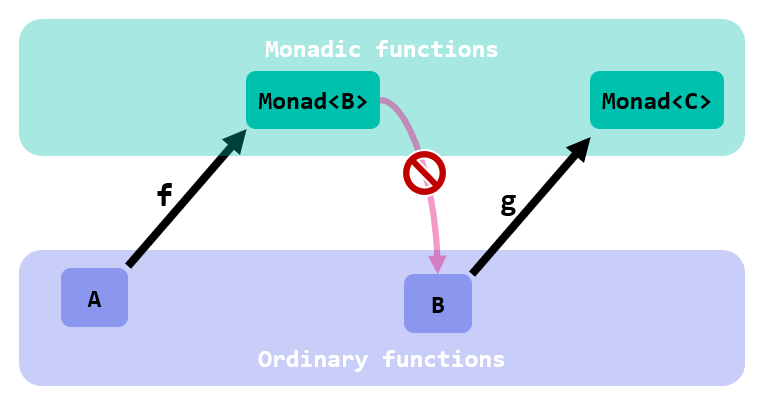
Your problem is: you would like to feed f with a value of A, but you don’t have it; instead, you have a value of Monad<A>.
You also know that the solution is the function bind.

Monad<B> Bind<A, B>(Func<A, Monad<B>> f, Monad<A> a) => ...

that is, a function with the signature:

//             f            input   =>  output
bind :: (A -> Monad<B>) -> Monad<A> -> Monad<B>

Here’s the little new intuition you have to develop: instead of seeing to bind as the function to feed f with input to get an output, that is, as the monadic version of Apply, imagine surronding the last 2 elements in parenthesis:

//             f        => (  input   -> output   )
bind :: (A -> Monad<B>) -> ( Monad<A> -> Monad<B> )

Graphically: you start from a monadic function f:

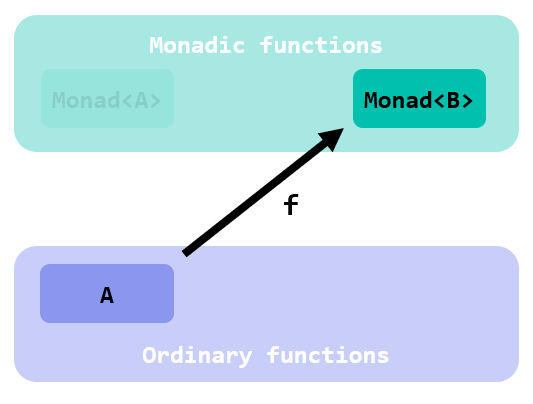
and this is what you get applying bind:

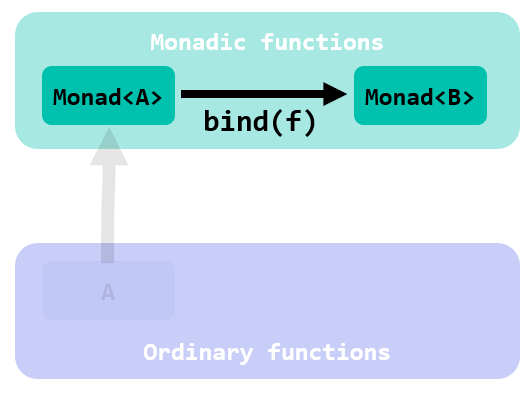
That is: imagine bind as that function that, given a function:

f :: A -> Monad<B>

transforms it so its type signature becomes:

f' :: Monad<A> -> Monad<B>

You like f' a lot! Remember your problem?

You would like to feed f with a value of A but you don’t have it;
instead, you have a value of Monad<A>.

That’s perfect: the function bind gave you back a function that wants a Monad<A> as input. bind solved your problem.

Here’s the gist. bind transforms a series of not type-compatible monadic functions:

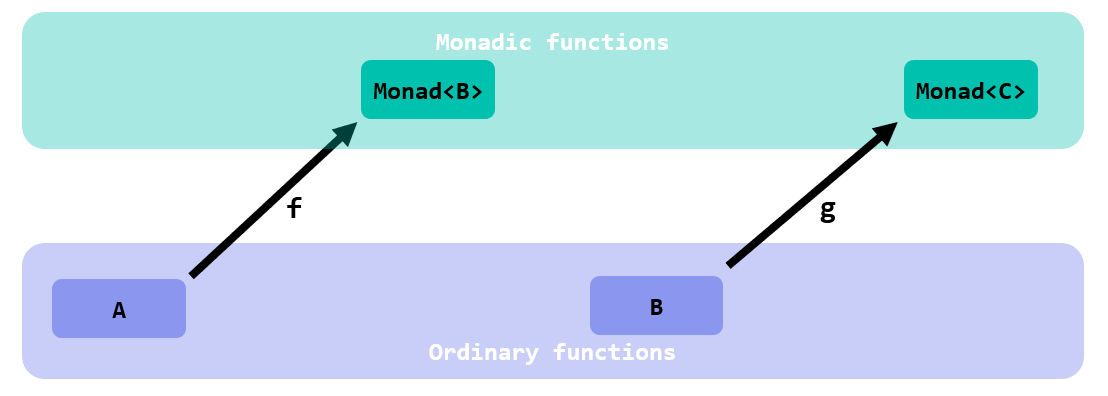
lifting their input types so that they can be bound and composed together:

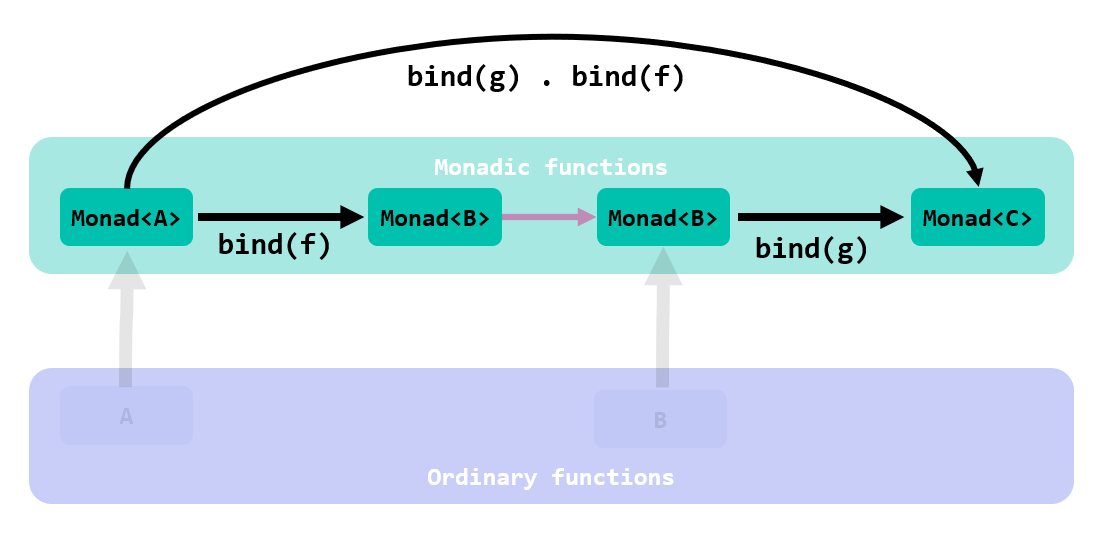
In other words: you know there are benefits in working in the monadic world; bind takes those function that are still with one of their legs in the ordinary world and it elevates them.

Completing this with return and run, it’s intuitive to think that the core pattern adopted in programming functionally with monads is the following:

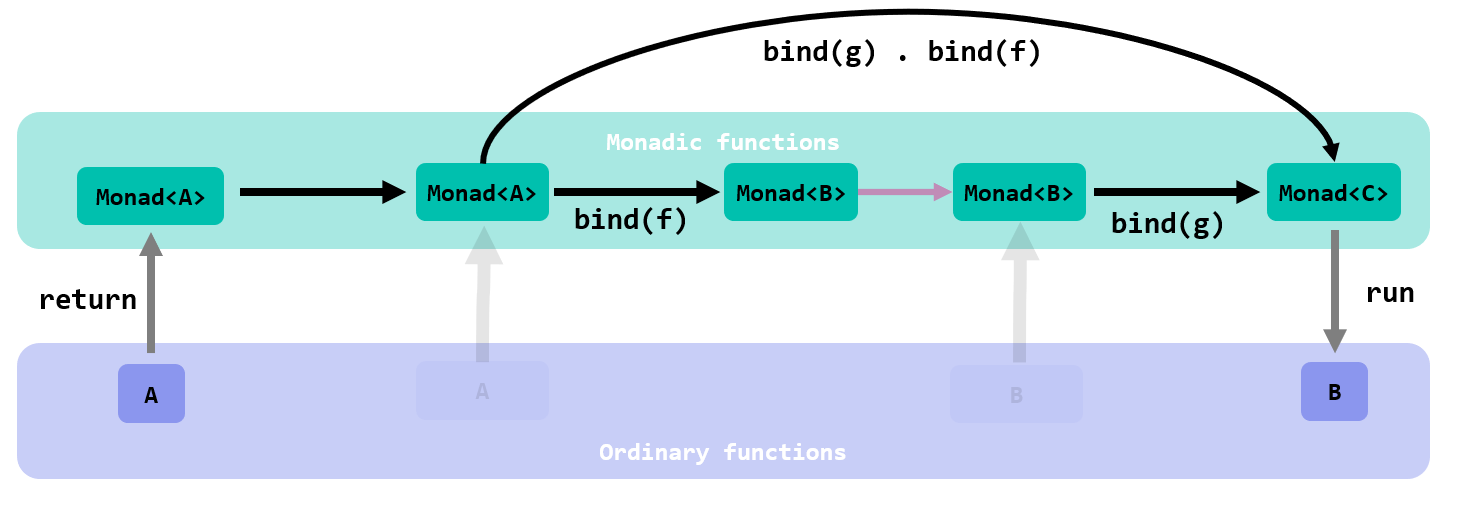
• You start by elevating your input value to the monadic world with return.
• You process it with a series of monadic functions, bound with Bind.
• And finally, at the edge of your application, you descend down to the world of ordinary functions and values, with run.

Show me the code or shut up!

Remember the implementation of Bind for the IO Monad?

IO<B> Bind<A, B>(this Func<A, IO<B>> f, IO<A> a) => 
    new(() => f(a.Run()).Run());

Its signature is

(A -> IO<B>) -> IO<A> -> IO<B>

To make it implement:

(A -> IO<B>) -> (IO<A> -> IO<B>)

you just have to move the IO<A> a parameter out of the function parameters, and to adapt the returning type:

Func<IO<A>, IO<B>> Bind<A, B>(this Func<A, IO<B>> f) => (IO<A> a) =>
        new(() => f(a.Run()).Run());

The implementation needn’t change.
Similarly, for the Maybe monad, the original Bind:

Maybe<B> Bind<A, B>(Func<A, Maybe<B>> f, Maybe<A> a) =>
    a.Run(
        just: a => f(a),
        nothing: () => new Nothing<B>());

can be rewritten as:

Func<Maybe<A>, Maybe<B>> Bind<A, B>(Func<A, Maybe<B>> f) => (Maybe<A> a) =>
    a.Run(
        just: a => f(a),
        nothing: () => new Nothing<B>());

Notice that they don’t need to be methods of a monad instance, as they don’t depend on a value anymore. They can be easily static, or even Extension Methods of Func:

internal static class MaybeExtensions
{
    internal static Func<Maybe<A>, Maybe<B>> Bind<A, B>(this Func<A, Maybe<B>> f) => (Maybe<A> a) =>
        a.Run(
            just: a => f(a),
            nothing: () => new Nothing<B>());
}

Here’s how it is used:

Func<string, Maybe<int>> length = s =>
    s == null
        ? new Nothing<int>()
        : new Just<int>(s.Length);

// here we are elevating the function
var elevatedLength = length.Bind();

// so we can feed it with a monadic value
Maybe<int> monadicResult = elevatedLength(Return("foo"));

var result = monadicResult switch
{
    Nothing<int> => "got nothing",
    Just<int> { Value: int value } => $"got a {value}"
};

Assert.Equal("got a 6!", result);

Notice how the code uses switch as the native way to run the monad.

Functors

Take a break. It was a short but intense journey. Ruminate on this intuition, give yourself the time to assimilate the notion of bind as a combinator.

You are ready to understand Functors: it will be a matter of defining a different combinator: map.

Proceed to Chapter 8.

Comments

GitHub Discussions