In which you make C# nondeterministic

I hope you enjoyed your ice-cream.
Without much ado, let’s get our hands dirty with a new use case for monads. That could sound puzzling, at first, but I swear that it is simple: nondeterministic functions.

Nondeterministic functions

In this context, nondeterminism does not mean randomness — which, by the way, is also supported by monads.
If a deterministic function represents a single path from an input to a specific outcome:

int IWillAlwaysCalculateTheDouble(int n) => n * 2;

a nondeterministic function represents an execution stemming into many paths, each yielding possibly different outputs:

int IAmUndecided(int n) => ... // maybe n*2, maybe n*3, maybe n*4

Nondeterministic is a misleading term: our nondeterministic functions are still pure and referential transparent: they consistently produce the same outputs for the same inputs. However, they are used to model uncertainty.
Think to a function that given a specific position in a maze returns the information:

From here you can either go forward, to the left or to the right: 
either paths are legit.
I'm not going to take a decision on a specific path.

Or think to a function describing the probability distribution of a stocastic process, such as the fluctuation of stock prices: the function might model a Gaussian bell shaped curve and even if it does not return a single value you still want to compose it with other similar functions.

Unsurprisingly, nondeterministic functions are typically leveraged to explore combinatory problems, such as the evaluation of the possible moves in a chess match.
And that’s exactly the use case we will develop (although in an extremely simplified implementation).

Modeling nondeterminism

Imagine a pure, deterministic function that given the position of a knight on a chess board, moves it to a different, legit position:

moveKnight :: Position -> Position

A trivial way to model moveKnight as a nondeterministic function is to let it return multiple paths:

moveKnight :: Position -> IEnumerable<Position>

That’s absolutely correct, and you will find many tutorials implementing nondeterminism with Monads this way.
Yet, I think this is a missed opportunity to understand some small — yet important — minutiae. Allow me then to proceed differently.

Following our initial idea to devote a dedicated monadic type to each specific source of effects / extra-behavior, let’s imagine to have a Nondeterministic type:

moveKnight :: Position -> Nondeterministic

Of course, nondeterminism on integers is different from nondeterminism on Positions, so we’d better have a type parameter for our monad:

moveKnight :: Position -> Nondeterministic<Position>

Finally, let me please shorten hereinafter Nondeterministic with Nond:

moveKnight :: Position -> Nond<Position>

The List monad is just a simplification

What does Nond<Position> mean?
It models the fact that moveKnight is undecided which Position the algorithm should select. It treats this undecision as a source of impurity: therefore, it returns a monadic value. Doing so, the problem of enumerating all the possibilities is deferred. When the monad is eventually run, the enumeration will be unrolled.
Until then, all that the Nond<Position> monad does is to provide the programmer with a way to compose and bind other similarly nondeterministic functions, via the classsical and standardized interface of a monad, without loosing information about the source of nondeterminism.

Now, how to structure Nond<A>? It’s only natural to model the multiple possible values as a collection of values of type A.
In fact, you could have just used a list for representing nondeterministic computations. It’s indeed a classical approach. But it does not tell the whole story: lists are only one of the many ways to model nondeterminism.

A decimal -> Nond<decimal> representing the forecast price of a stock is likely to return values following a Gaussian distribution. From this perspective, IEnumerable<decimal> would be a broken model, because it corresponds to a uniform distribution of equally probable prices, and this poorly model the reality.

In implementing Nond<decimal>, you could easily decide to store the mean and the variance, rather than a collection of possible prices. The Nond monad is all about abstracting the nondeterministic effect away, so that your code can be made independent from it. What is important, for your implementation, is that given 2 functions built around the notion of a Gaussian distribution (or whatever else notion of nondeterminism), their combination is done in a way that preserves some specific statistical rules.

The take aways are:

• the articles and tutorials stating that “List is a monad for modeling nondeterministic computations” are surely right, but they tell half the story. By no means this implies that Lists are the only way for modeling nondeterminism.

• If your Nond<decimal> must implement some logic about the Gaussian distribution, this means that Monads aren’t just a mechanical stratagem for combining type-uncompatible functions ; they are in fact a design tool for type-modeling the business domain. They do implement domain logic.

If you are going to embrace Functional Programming, you are going to invent a lot of new monads.

Implementing the Nond monad

We left with:

moveKnight :: Position -> Nond<Position>

For the sake of simplicity:

• To represent a position, we’ll just use a pair of integers (int, int).
• We will not raise errors if the knight moves outside the board: (100, 100) is just as fine as (5, 5).
• We consider all the positions as equally probable and legit.

So we can be prosaic and opt for a simple IEnumerable of (int, int).
Considering how a knight moves:

this is a possible implementation for move:

using Position = ValueTuple<int, int>;

Func<Position, Nond<Position>> move = currentPosition =>
{
    var (x, y) = currentPosition;
	
    return new Nond<Position>(new[]
    {
        (x + 1, y + 2),
        (x - 1, y + 2),
        (x + 1, y - 2),
        (x - 1, y - 2),
        (x + 2, y + 1),
        (x - 2, y + 1),
        (x + 2, y - 1),
        (x - 2, y - 1)
    });
};

Let’s first see how such a monad could be used. Then, we will deep dive into the details of the implementation.

Using the monad

Let’s see how to use Bind (yes: from now on, we are calling Apply as a Haskell programmer would).
Starting from position (5, 5) we apply move over and over, passing the result of the one call to the next one with Bind:

Position start = (5, 5);
Nond<Position> step1 = move(start);
Nond<Position> step2 = move.Bind(step1);
Nond<Position> step3 = move.Bind(step2);

Using LINQ (we will learn this soon!) we can write the code as:

from s1 in move(start)
from s2 in move(s1)
from s3 in move(s2)
select s3;

To give you a sense of the flexibility, here’s how to calculate the 1.073,741,824 possible destinations (741 of which are unique) for a knight starting from (5, 5) after 10 steps:

var startingPoint = new Nond<Position>((5,5));
var steps = 
    Enumerable.Range(1, 10)
        .Aggregate(startingPoint, (current, _) => move.Bind(current))
        .Run();

Assert.Equal(1_073_741_824, steps.Length());
Assert.Equal(741, steps.Distinct().Length());

Just like with the IO Monad, our client code knows from the type-system that there is an extra-computation, but does nothing in particular to deal with it other than using the monadic Bind.

Implementing the monad

We will implement the Nondeterministic monad in 5 simple steps:

• The skeleton of the Nondeterministic type, for holding the needed information.
• A new function Return, as a way to lift values to the nondeterministic realm.
• Run, to unroll all the possible combinations.
• Bind, to link functions.
• Compose, which we assume will be based on Bind.

Type skeleton

Here’s the minimum of Nond to make the compiler happy:

record Nond<T>(IEnumerable<T> Items)

Return

That’s indeed a new topic, which deserves a little detour.
Read again our original client code:

Position start = (5, 5);

Nond<Position> step1 = move(start);
Nond<Position> step2 = move.Bind(step1);
Nond<Position> step3 = move.Bind(step2);

You might dislike that it’s not completely consistent: the first time move is invoked with the native C# function application; then, Bind is used.
We could be more symmetric if only the starting position was nondeterministic too. Now, think about it: nothing prevents us from having a function that, given a single value, returns the same value in a nondeterministic context. Something like:

Nond<Position> BuildMonad(Position p) =>
    new Nond<Position>(new []{ p });

This would allow you to write:

Nond<Position> start = BuildMonad(5, 5);

Nond<Position> step1 = move.Bind(start);
Nond<Position> step2 = move.Bind(step1);
Nond<Position> step3 = move.Bind(step2);

Interpret this like the following:

• The knight starts from (5, 5).
• We know we are going to explore all the possible combinations; we know we are going to operate in a nondeterministic context.
• Then, we use BuildMonad to lift the deterministic position (5, 5) to a non deterministic context.
• BuildMonad returns an instance of Nond<Position>. This already belongs to a world where all our functions will keep exploring the knight movement paths. We can procede binding functions after functions.

Here’s a test for BuildMonad:

Position position = (5, 5);
Nond<Position> monadicPosition = BuildMonad(position);

IEnumerable<Position> allCombinations = monadicPosition.Run();
        
Assert.Equal(1, allCombinations.Length());
Assert.Equal(new [] { position }, allCombinations);

To grasp the gist of this little BuildMonad, compare it with the identity function:

Nond<Position> BuildMonad(Position p) =>
    new Nond<Position>(new []{ p });

Position Identity(Position p) =>
    p;

• Feed Identity with a position and it will give it you back, unmodified. Identity is a pure, honest, deterministic function.
• Feed BuildMonad with a position and it will give it you back, unmodified, but together with a monadic structure. This makes BuildMonad a nondeterministic function. But pretty similar to Identity.

That’s a funny function, if you think about it. Its signature claims it is nondeterministic: it should be undecided which position to return. But in fact, it is not: it returns only one position.

You can think of it as the simplest possible case for a nondeterministic function. As a matter of facts, it is deterministic but its type signature lets it operate in a Bind chain, in an nondeterministic context. It is a deterministic function acting like it was nondeterministic.

Here’s the takeaways:

• Return is the monadic version of the Identity function.
• It is traditionally called return.
• By definition, bind and return are the minimal implementation of any monads.

In the case of the IO monad, return is a function lifing a value in a side-effect context, and performing no side-effects at all:

IO<T> return(T value) => 
    new IO(() => value);

In OOP languages like C#, return is typically just the constructor of the monad class. Just as simple.
In the case of the Error monad, which models a context where functions can generally fail returning errors, it would lift a value in a function just not failing at all.

In other words, return is the elevator to the monadic world.
Yes, I agree with you: return is a horrible and misleading name. As mentioned in Why does a monad use “return” or “unit” rather than “lift”? it’s called like this only for historical reasons.
Not my fault, I swear.

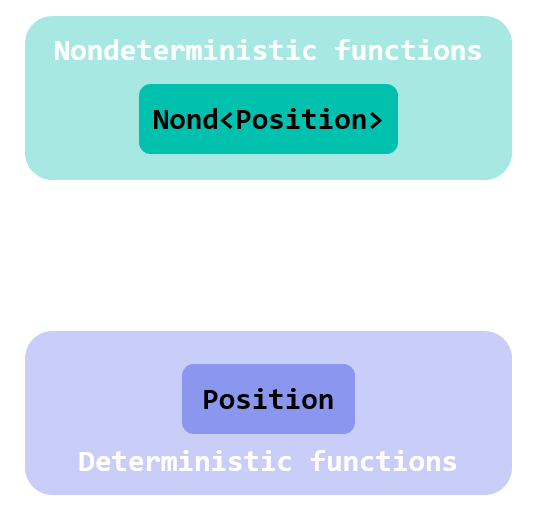
A tale of 2 worlds

Let me offer you a different prespective on return.
In Part 1 I mentioned the distinction between honest and dishonest functions; we saw how monadic functions — returning their output together with a dedicated type representing a specific kind of impurity — allow us to deal with impurity with pure functions.

For the case of nondeterministic functions, it is only fair to group functions in 2 separate worlds: one populated by the ordinary functions and values, and one where functions and values, handled via the Nond monadic type, convey the notion of nondeterminism:

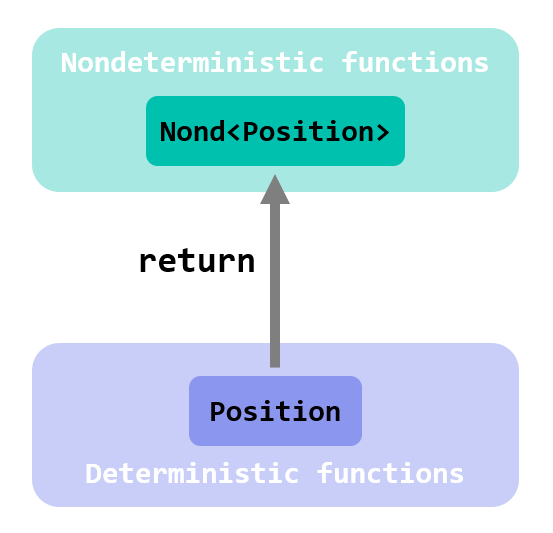
With this perspective in mind, return can be interpreted as the function that lifts a value to the world of nondeterministic functions:

run does the opposite: given a value in the world of nondeterministic functions, it projects the undeterminism down, returning back all the possible combinations expressed as an ordinary, non-monadic type.

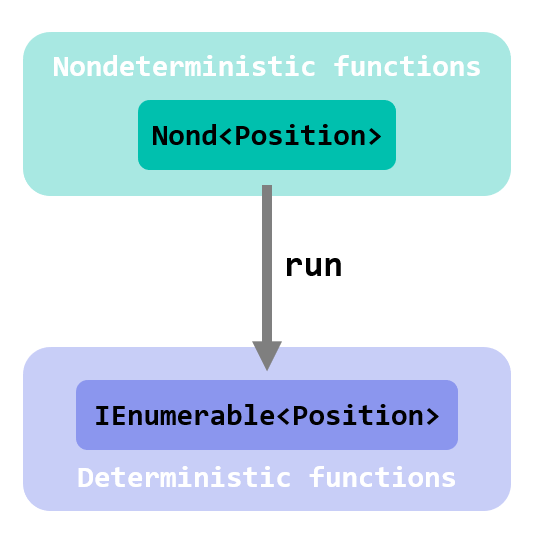
Notice that return and run are not perfectly symmetric: run does not return back a single Position, but a collection.

The notion of binding and combining monadic functions aligns to the idea of:

• starting from the world of the ordinary functions
• lifting to the elevated world of the nondeterministic functions
• operating in that world, using Bind and Compose (and other functions we will soon discover)
• and finally descending back to the world of ordinary functions with run

Nothing prevents us from extending this visualization to other monadic function types. In the general case:

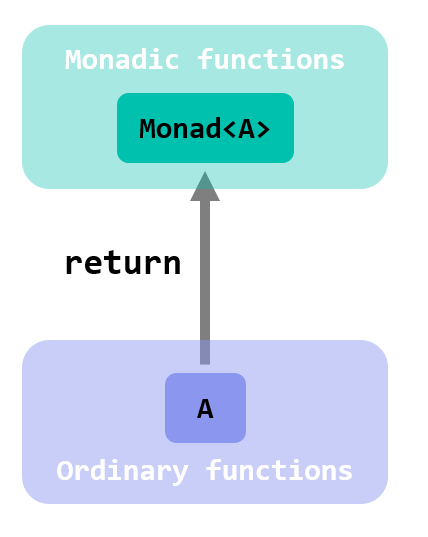
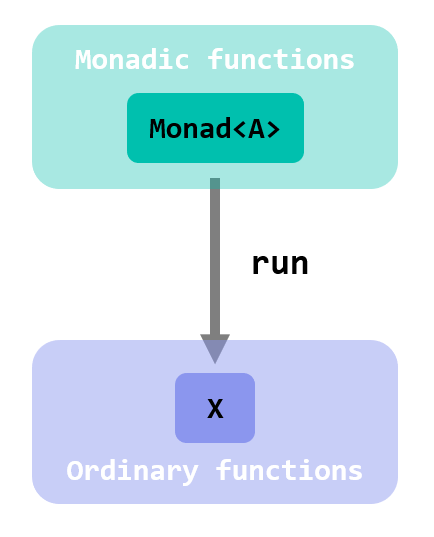
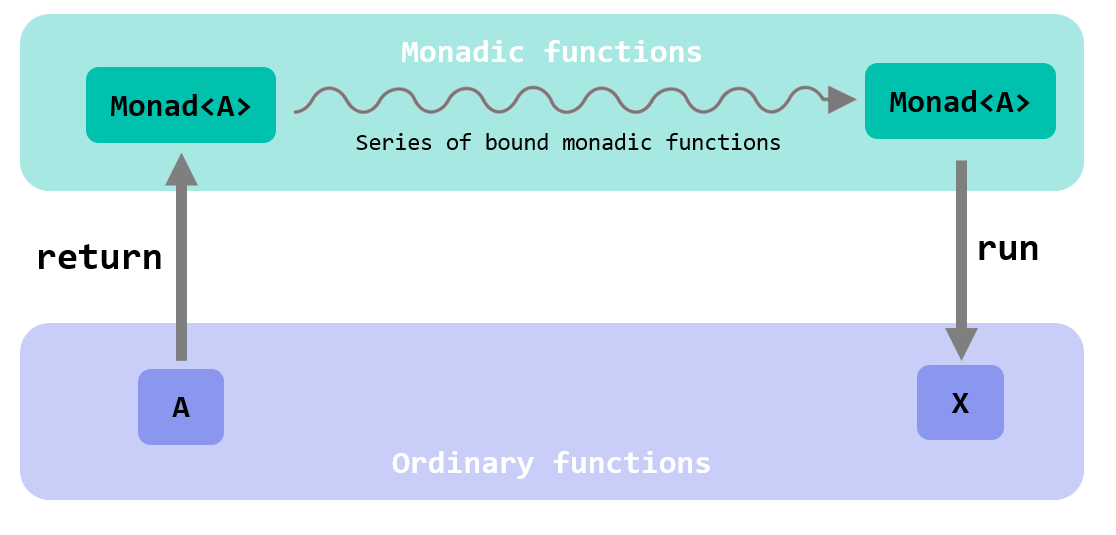
Notice, again, that descending from a Monad<A> with run to the world of ordinary functions and values not necessarily returns an A.

It turns out that this interpretation is also of great help to understand Bind and the other functional combinators we are going to introduce. Stay tuned: we’ll come back to this in a couple of pages.

Run

Implementing run for the Nondeterministic monad should be easy. Given the skeleton we built:

record Nond<T>(IEnumerable<T> Items)

running the monad should be a matter of returning to the caller all the possible, accumulated combinations:

record Nond<T>(IEnumerable<T> Items)
{
    internal IEnumerable<T> Run() => Items;
}

Seriously?
Yes, that’s all.

Bind

Ok! This is just a bit more challenging.
Let’s recap what bind was for. Imagine you executed a nondeterministic function. By its nature, it returned a nondeterministic value:

Nond<string> nondeterministicValue = previousFunction("foo");

Now, consider a function f asking for a deterministic string, not a Nond<string>:

Func<string, Nond<int> f => ....

You can’t directy pass nondeterministicValue to f. You need bind.
bind has the following signature:

Nond<int> bind(
    Func<string, Nond<int> f, 
	Nond<string> value) => ....

Just like the IO case, implementing it is a matter of executing Run in a deferred way:

internal static Nondeterministic<B> Bind<A, B>(
    this Func<A, Nondeterministic<B>> f, 
    Nondeterministic<A> m)
{
    IEnumerable<A> values = m.Run();
    IEnumerable<Nondeterministic<B>> mappedNested = values.Select(f);
    IEnumerable<B> flat = mappedNested.SelectMany(m => m.Run());
    return new Nondeterministic<B>(flat.ToArray());
}


Nond<int> PreviousFunction() =>
    new Nond<int>(new[]
    {
        1,
        2
    });

Func<int, Nond<(int, char)>> g = j =>
    new Nond<(int, char)>(new[]
    {
        (j, 'a'),
        (j, 'b')
    });

Nond<int> nondValue = PreviousFunction();

Nond<(int, char)> bind = g.Bind(nondValue);

IEnumerable<(int, char)> combinations = bind.Run();
Assert.Equal(new[] { (1,'a'), (1, 'b'), (2, 'a'), (2, 'b') }, combinations);

Compose

Deriving the Function composition from Bind reserves a nice suprise.
The logic is:

• We need to generate a new function A -> C, therefore we return a lambda (A a) => ....
• a can be directly fed to the innermost function, g.
• This gives us back a nondeterministic value of B.
• That cannot be directly used to feed f: we need to use Bind for this.
• Bind returns a nondeterministic C, which is the final value.

Func<A, Nond<C>> Compose<A, B, C>(Func<B, Nond<C>> f, Func<A, Nond<B>> g)
{
    return a =>
    {
        Nond<B> nondB = g(a);
        Nond<C> nondC = f.Bind(nondB);
        return nondC;
    };
}


Func<Position,Nond<Position>> composed = Compose(move, move);

Position start = (5, 5);
IEnumerable<Position> allPossiblePositions = composed(start).Run();

Assert.Equal(64, allPossiblePositions.Length());

Reminds you of anything? Compare it with the Compose we distilled for the IO Monad in part 4:

Func<A, IO<C>> Compose<A, B, C>(this Func<B, IO<C>> f, Func<A, IO<B>> g)
{
    return a =>
    {
        IO<B> ioB = f(a);
        IO<C> ioC = g.Bind(ioB);
        return ioC;
    };
}

Besides the types, they are exactly the same! Inline each intermediate variable and you would get for both

Func<A, Monad<C>> Compose<A, B, C>(Func<B, Monad<C>> f, Func<A, Monad<B>> g) => 
    a => f.Bind(g(a));

Seems like we discovered a universal law, a general rule which is presumibly valid for all the possible monads.
Indeed, in Haskell the monadic function composition (slighly simplified) implementation is:

(<=<) :: (b -> m c) -> (a -> m b) -> (a -> m c)
g <=< f = \a -> g a >>= f

This is an incredibly remarkable result: not only did we provide the same interface Bind + Return to all the monads, no matter which kind of inpurity they model; but now we are even discovering some universal laws and combinators, that are also indipendent from the extra-computation.
Isn’t this astonishing? You still have to invent and implement the monads you will use in your future code and you already know the formula for deriving their Compose combinator, knowing it will perfectly work with them.

Wrapping up

Here’s what we found out:

• All the monadic types share the same interface: Bind and Return.
• Return lifts values in the monadic world.
• There also must be a way to discend back to the non-monadic world: Run.
• Each monad has got its peculiar implementation of Bind, Return and Run.
• It seems that other functionalities are derived from Bind, Return and Run. They are likely to be universal.
• A graphical representation of the non-monadic and the monadic world could help us develop a useful intuition.

There are few other topics I would like now to tackle:

• A last monadic function example: functions that might fail returning a value. I hope this will persuade you that crafting new monads for your future requirements isn’t too challenging.
• A short detour on Functors. This will enable you to connect the dots and to ultimately achieve a unified understanding.
• A more comprehensive representation of the functional combinators, using the just introduced graphical notation.
• A little experiment in which we replace Nond<A> with IEnumerable<A>. This will give you an unexpected revelation: C# natively supports monads.

Go to Chapter 6;

References

• Why does a monad use “return” or “unit” rather than “lift”?
• Haskell composition of Kleisli arrows. (>=>), with flipped arguments

Comments

GitHub Discussions